本文摘抄自公众号:优化算法交流地
MATLAB调用CPLEX的方法来自:http://blog.sina.com.cn/s/blog_b041fdcb0102ydsq.htm。该篇博文中附有相应的安装文件,除了需要安装CPLEX以外,还需要安装YALMIP建模软件包,这是一个在MATLAB上进行数学建模超级方便的工具包,有了YALMIP可以大大降低建模的难度。具体如何操作?该怎么样进行联合开发呢?本文以CVRP问题为例进行展示。
值得注意的是:只有按照步骤安装好YALMIP和CPLEX,并且在MATLAB中配置好相应的路径后,才能正确运行程序。
因此,本文以求解CVRP标准算例问题为例,来演示MATLAB+YALMIP+CPLEX的求解效果,具体代码如下。
clear
clc
vNum=5; %车数量
cusNum=13; %总节点数量
C=6; %单车容量
demands=[0,1.2,1.7,1.5,1.4,1.7,1.4,1.2,1.9,1.8,1.6,1.7,1.1]; %需求量
x=[81.5,87,75,85,89,77,76,87,73,77,73,91,92];
y=[41.5,37,53,52,41,58,45,53,38,38,31,47,44];
axis=[x' y']; %城市坐标
% Dij = zeros(cusNum);%计算城市之间的距离
D=pdist(axis);
Dij=squareform(D); %距离矩阵,满足三角关系,暂用距离表示花费c[i][j]=dist[i][j]
%% 决策变量
Xijk=binvar(cusNum,cusNum,vNum,'full');%i、j节点之间是否由第k辆车进行配送
Yik=binvar(cusNum,vNum,'full'); %k辆车是否经过i节点
Uik=sdpvar(cusNum,vNum,'full'); %Uik表示车辆k在访问i节点后,车子的剩余容量
%% 目标函数
obj=0;
for i=1:cusNum
for j=1:cusNum
for k=1:vNum
obj=obj+Dij(i,j)*Xijk(i,j,k);
end
end
end
f=obj;
%% 约束条件
F=[];
for i=2:cusNum
F=[F;sum(Yik(i,:))==1]; %每个需求点i都会被一辆车经过
end
for i=1
F=[F;sum(Yik(i,:))<=vNum];%配送中心则会被所有用到的小车经过
end
for k=1:vNum
F=[F;sum(demands(:).*Yik(:,k))<=C]; %每个回路上的需求量之和小于车的容量
end
for i=1:cusNum
for j=1:cusNum
for k=1:vNum
if i==j
F=[F;Xijk(i,j,k)==0]; %不可能存在从该点出发又回到该点的情况
end
end
end
end
for i=1:cusNum
for k=1:vNum
F=[F;sum(Xijk(i,:,k))==sum(Xijk(:,i,k))];%流量平衡
end
end
% for j=2:cusNum
for j=1:cusNum
for k=1:vNum
F=[F;sum(Xijk(:,j,k))==Yik(j,k)];%Xijk和Yik的关系
end
end
for i=1:cusNum
for k=1:vNum
F=[F;sum(Xijk(i,:,k))==Yik(i,k)];%Xijk和Yik的关系
end
end
for i=2:cusNum
for j=2:cusNum
for k=1:vNum
if i~=j
if demands(i)+demands(j)<=C
F=[F;Uik(i,k)-Uik(j,k)+C*Xijk(i,j,k)<=C-demands(i)];%Xijk和Ui
end
end
end
end
end
for i=2:cusNum
for k=1:vNum
F=[F;Uik(i,k)<=C];
F=[F;Uik(i,k)>=demands(i)];
end
end
%% 求解
ops = sdpsettings( 'solver','cplex');
sol=solvesdp(F,f,ops);
f=double(f);
Xijk=double(Xijk);
Yik=double(Yik);
Uik=double(Uik);
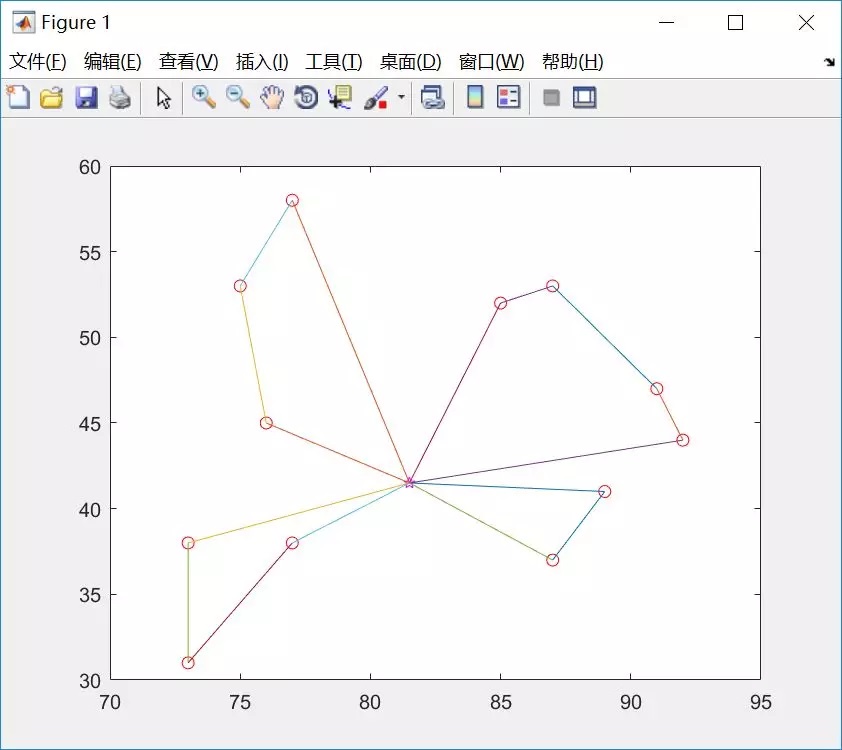
%% 画图
plot(axis(2:cusNum,1),axis(2:cusNum,2),'ro');hold on;
plot(axis(1,1),axis(1,2),'pm');hold on;
for i=1:cusNum
for j=1:cusNum
for k=1:vNum
if Xijk(i,j,k)==1
plot([axis(i,1),axis(j,1)],[axis(i,2),axis(j,2)],'-');
end
end
end
end
for k=1:vNum
[a,b]=find(Xijk(:,:,k));
sqe=[a,b];
sqe1=zeros(1,0);
sqe1(1)=1;
[a,b]=find(sqe(:,1)==1);
for i=2:length(sqe)+1
[a,b]=find(sqe(:,1)==sqe1(i-1));
sqe1(i)=sqe(a,b+1);
end
disp(['车辆',num2str(k),'的路径如下:']);
disp(sqe1)
end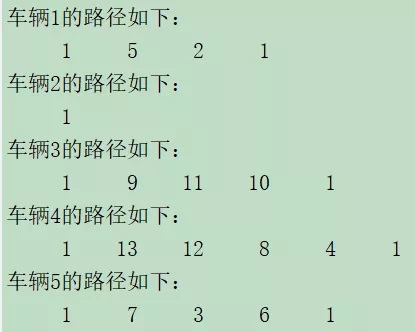
本文共 366 个字数,平均阅读时长 ≈ 1分钟





评论 (0)